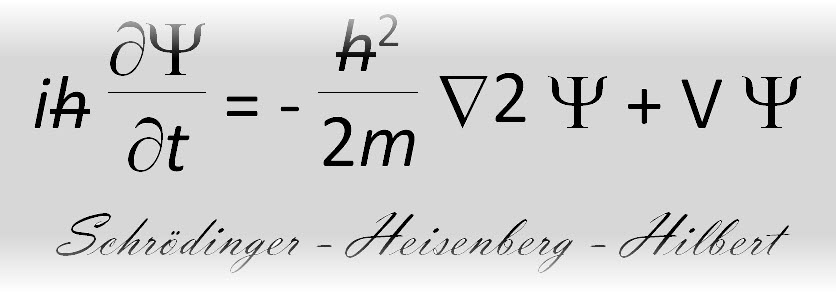I premi Nobel per la fisica non sono tutti uguali e quello del 2022 appartiene alla categoria di quelli speciali perché va a premiare la fase II della Meccanica Quantistica.

Il superpremio sarebbe spettato a John Bell (1928-1990) ma lui è morto improvvisamente quandio aveva solo 62 anni. Ha fatto in tempo a vedere l’affermazione delle sue idee ma il premio no; lo si dà solo a fisici in vita e capita spesso che i riconoscimenti arrivino in ritardo (è successo anche ad Einstein).

Così Bell non ha fatto in tempo e il premio, anziché ad un fisico teorico è andata a tre fisici sperimentali, anche se Zeilinger, per gli studi sulla informatica quantistica, il teletrasporto e l’entanglement su sistemi a più di due particelle si colloca a metà strada tra fisica teorica e sperimentale.
I tre vincitori del premio hanno grosso modo la mia età e ciò per un verso mi preoccupa e per l’altro mi consola. Il fatto che mi preoccupi sta nel trascorrere degli anni e i fisici sanno che “la freccia del tempo” non cambia verso; la consolazione viene dal fatto che dopo aver iniziato ad approfondire la fisica, inclusa la MQ, mi chiedevo spesso se si trattasse di un circolo chiuso e ormai compiuto.

Quando ho iniziato a ragionare di queste cose erano passati una cinquantina d’anni dal completamento della MQ e si aveva la impressione che, rispetto ai fondamenti, fosse rimasto poco da dire. E’ vero c’erano state delle voci nel deserto, ma avevano poco credito.

In realtà, in giro per il mondo c’erano dei fisici coraggiosi che continuavano a farsi delle domande. Racconta Aspect che, quando incontrò per la prima volta John Bell e gli espose la sua volontà di inventare un esperimento che consentisse di verificare la correttezza delle sue idee, come prima domanda ebbe la richiesta ironica se avesse un posto di ruolo.

Lo stesso John Bell, che coltivava certe “insane passioni”, da sempre dedicava alla riflessione sui fondamenti il tempo libero e per il resto faceva i suoi calcoli sugli aspetti di fisica aplicata connessi al funzionamento del grande acceleratore di Ginevra. Forse Aspect era la persona giusta visto che si interessò al tema dell’entanglement dopo aver trascorso qualche anno del suo post laurea in Camerun a fare del volontariato sociale e fu in Africa, munito della Bibbia di Claude Cohen-Tannoudji (Quantum Mechanics), che iniziò a farsi delle domande. Un altro dr. Bertlmann.

Con questo premio Nobel si è chiuso un cerchio e, per questa ragione mi sono preso la briga di fare una seconda opera di traduzione. L’articolo che vi presento, scritto per un convegno organizzato da Zeilinger per onorare i 50 ani dalla pubblicazione (nel 1964) dell’articolo di John Bell sull’entanglement ha un duplice pregio:

• riassume il nocciolo delle tematiche delle diseguaglianze di Bell (e dunque vi consentirà di digerire meglio la treattazione che ne ho dato nel capitolo 0606)
• entra nel merito delle problematiche vere che un fisico sperimentale si pone di fronte alla neccessità di verificare la correttezza di una legge

E’ stato un lavoraccio perché ho scelto di non riassumere nulla e di lasciare intatto anche tutto l’apparato bibliografico. Alain Aspect

• riepiloga ampiamente tutto il lavoro di Bell;
• racconta gli esperimenti che hanno preceduto i suoi;
• entra in dettaglio sulle problematiche che si è posto e sulla necessità di dare delle risposte agli avversari delle diseguaglianze di Bell pronti ad inventarsi “scappatoie” (loop-hole) di tutti i generi (e se i fotoni, dotati di una intelligenza superiore scoprissero che l’apparato sperimentale non è genuinamente casuale e riuscissero a comunicarsi il da farsi?)
• ci informa su quello che è stato fatto dopo

Una buona occasione per capire cosa voglia dire fare degli esperimenti veri: i fotoni non si trattano uno alla volta ma ne servono milioni al secondo; come si maneggiano le cascate radiative (!?!) in un periodo in cui i laser che servono per eccitare gli atomi di Calcio sono molto primitivi, bisogna distinguere i fotoni sporchi da quelli buoni; bisogna cambiare il funzionamento dell’apparto mentre i fotoni sono in volo e si parla di nanosecondi, …

Buona lettura: – Il teorema di Bell – la visione ingenua di un fisico sperimentale di Alain Aspect

Il corso di fisica – le news e gli aggiornamenti del corso – Il capitolo 0606 Meccanica quantistica II parte

La apertura del capitolo è dedicata ai 6 postulati che costituiscono la ossatura della intera MQ e vedrete che si leggono con piacere e senza bisogno di appelli né alla fede né a competenze matematiche improponibili. Lo schema della teoria è semplice, accattivante anche se contro intuitivo.

Oltre ad enunciarli ho dedicato molta attenzione ad illustrarne il significato e a sottolinearne i nessi reciproci.

Il paragrafo successivo è interamente dedicato al principio di indeterminazione facendone vedere la dipendenza dalla struttura assiomatica della teoria. Tutte le coppie di operatori che non commutano, cioè tutte le coppie di operatori  e Ê e  per i quali ÂÊ – Ê risulta diverso da zero sono soggetti ad una indeterminazione quando si cerchi di determinarne simultaneamente il valore; tale indeterminazione è soggetta ad una medesima legge.

Il terzo paragrafo è interamente dedicato alla teoria quantistica del momento angolare una osservabile caratterizzata da una stranezza legata al tema della non commutazione: si tratta di un vettore per il quale sono determinabili una componente e il modulo mentre altre due sono libere e da queste regole seguono le caratteristiche del secondo e terzo numero quantico dei modelli atomici. Data la importanza del tema ho esplicitamente svolto i calcoli che si basano su una coppia di operatori detti di shift perché fanno crescere e decrescere di una stessa quantità i valori del momento angolare ogni volta che si usano.

Il quarto paragrafo tratta di quel particolare momento angolare detto spin che, rispetto ai momenti angolari orbitali, presenta il vantaggio di essere collocato in uno spazio di Hilbert a due dimensioni e di essere pertanto comodo da maneggiare.

Lo spin viene analizzato seguendo due approcci: una introduzione basata sulla esecuzione di esperimenti ideali alla Stern & Gerlach e una seconda trattazione classica basata sulla costruzione delle cosiddette matrici di Pauli, gli operatori introdotti da Wolfang Pauli subito dopo la scoperta dello spin per collocarlo all’interno della struttura teorica della Meccanica Quantistica.

Mentre mi documentavo qua e là, sullo spin ho trovato un testo che, seppur a livello elettronico, e non nucleare, si occupava della trattazione quantistica del fenomeno della risonanza degli spin, così mi è venuta l’idea di approfondire ed è saltato fuori un ampio paragrafo dedicato ai principi di funzionamento della risonanza magnetica nucleare che, in ossequio al politicamente corretto secondo cui la parola nucleare evoca fantasmi, negli states hanno iniziato a chiamare MRI magnetic resonance imaging.

Mi sono dedicato principalmente agli aspetti fisici di funzionamento fermandomi alla soglia degli algoritmi che consentono di trasformare i segnali elettromagnetici di riassestamento in immagini, ma ne è venuto fuori qualcosa di interessante e che raramente si ritrova in un corso di fisica.

La ultima parte del capitolo è dedicata ad argomenti che, quando mi sono laureato erano considerati cose da rompisctole, la discussione su alcuni aspetti strani e inattesi della Meccanica quantistica.

Si tratta di questioni nate intorno alle insoddisfazioni epistemologiche di Einstein che, senza mettere in discussione l’impianto della MQ che aveva contribuito a creare, trovava insoddisfacenti alcune conclusioni che avevano a che fare con il collasso della funzione d’onda quando si esegue una misura.

Per alcuni sistemi quantistici, caratterizzati dalla non separabilità, cioè dalla impossibilità di separare il sistema nei suoi singoli componenti, si verificano (a livello di esperimento mentale) fatti che Einstein definiva sinistri (o diabolici): la misura su uno dei componenti determinerebbe istantaneamente il valore della stessa grandezza sugli altri componenti del sistema a qualsiasi distanza essi si trovino.

La discussione su queste faccende, innescata da Einstein negli anni 30 del 900 è andata avanti come se quelli che ponevano certe questioni fossero dei rompiballe perché l’impianto della MQ era solido e i risultati lo stavano a dimostrare.

Ma tra la fine degli anni 60 e i primi anni 70 un fisico irlandese del CERN che, ufficialmente si occupava di acceleratori, ma nel tempo libero rifletteva sui fondamenti, tirò fuori un teorema del tutto generale (più generale della MQ) che consentiva di sottoporre ad indagine sperimentale l’intera questione.

Una ipotetica teoria realista, che bandisse le indeterminazioni attraverso variabili nascoste, che rispettasse il principio di località secondo cui nessuna informazione e interazione si può propagare a velocità superiore alla velocità della luce, avrebbe dovuto rispettare una determinata diseguaglianza che invece era disattesa dalla MQ.

Fu così che a partire dagli anni 70 iniziarono una serie di esperimenti di verifica del comportamento di sistemi entangled, quelli per i quali si prevedevano i comportamenti sinistri.

L’esperimento decisivo fu realizzato da una equipe francese guidata da Alain Aspect. Le insoddisfazioni di Einstein erano malposte. La MQ è intrinsecamente non locale e gli esperimenti le danno ragione.

Degli esiti ne tratterò in un altro capitolo perché questo viaggia verso le 70 cartelle che, per un capitolo sono tante.

Se arriverete sino in fondo vedrete che, questa volta, gli esercizi e i problemi sono davvero pochi. E’ stata una scelta consapevole; gli aspetti tecnici lasciamoli agli specialisti e cerchiamo invece di rendere consapevoli le persone del fatto che il mondo, su scala microscopica, presenta aspetti inattesi. Cambia la scala e cambiano le leggi.

Il corso di fisica – le news e gli aggiornamenti del corso – il capitolo 0606 la meccanica quantistica II parte

Illustrazione originale dell’articolo

L’articolo I calzini del dr. Bertlmann fa parte della raccolta di articoli di J.S. Bell di taglio epistemologico intitolata Speakeable and Unspeakeable in Quantum Mechanic.

Mentre lavoravo al secondo capitolo di MQ, per alleggerire un po’ mi sono letto l’articolo di Bell e ho deciso che valesse la pena di tradurlo per renderlo disponibile ad un pubblico italiano più ampio. Detto … fatto

La storia dei calzini spaiati è vera e fa parte delle bizzarrie del dr. Bertlmann per la serie 1968 e dintorni. Bell utilizza l’argomento per spiegare le correlazioni che hanno una origine nel passato anche se l’esempio rischia di essere vagamente fuorviante, perché le correlazioni quantistiche legate all’entanglement si attualizzano nel presente.

Bell e Bertlmann erano due persone fuori dal comune e basta vederli in questa foto del 1980 al CERN per capire che si trattava di due personaggi oltre che fuori dal comune anche fuori dagli schemi.

Bertlmann e Bell al CERN nel 1980

Oggi ho ripreso in mano l’articolo di Bell per festeggiare l’acquisto di “Modern Quantum Mechanic – from Quantum Mechanics to Entanglement and Quantum Information” di Bertlmann che utilizzerò per scrivere la parte finale  del II capitolo di MQ. Lo pubblicherò nei prossimi giorni in attesa degli ultimi paragrafi (le prove sperimentali della violazione quantistica della località, le applicazioni dell’entanglement alla crittografia, al teletrasporto e alla informatica quantistica).

Oggi ho finito la revisione dell’esistente e già così è un bel malloppone.

Il libro di Bertlmann l’avevo scaricato in pdf come faccio con i testi da selezionare in vista di un acquisto e oggi ho deciso di regalarmi per Natale il cartaceo. Su 1000 pagine ce ne sono ben 700 dedicate agli sviluppi recenti della MQ. Che bello sarebbe stato avere il professor Bertlmann, nella primavere del 68, a tenere il corso di Istituzioni di Fisica Teorica… al posto del professor Prosperi che non capiva le nostre domande impertinenti.

Ma che dico?  Bertlmann è’ un mio coetaneo. E’ nato nel 1945 e dunque, ha un anno più di me e nel 68 muoveva i primi passi da studente; il suo dottorato è del 1974 … e si è sposato con una delle leader del movimento femminista austriaco, Renate. Ha scritto anche un importante testo di tipo critico sulla elettrodinamica quantistica.

Che bello questo ritorno a Vienna; la università di Boltzmann, di Mach e poi del circolo  che porta il nome della città. e che ha segnato una svolta nei miei riferimenti culturali generali e poi politici. Questo libro me lo terrò caro.

Segnalo che c’era un errore nel link al primo dei due capitoli di MQ che lo rendeva irraggiungibile. Ho corretto ma lo ripubblico qui Capitolo 0605

Il corso di fisica – le news e gli aggiornamenti del corso –L’articolo di John Bell – i calzini del dr Bertlmann

Inizialmente avevo pensato che, per sbrigarmela con la meccanica quantistica in un corso di Fisica Generale, sarebbe bastato un solo capitolo ma non è andata così. I capitoli, abbastanza corposi, sono diventati due e probabilmente per dare conto di tutti gli sviluppi più recenti diventeranno tre.

Questo primo capitolo, nella prima parte riprende la parte introduttiva che avevo scritto quando ancora insegnavo (nel 2007). L’idea è quella di fornire un quadro di quella fase incasinata iniziata a fine XIX secolo e proseguita sino ai primi due decenni del XX.

Dopo che con gli sviluppi della sintesi maxwelliana dell’elettro‌magnetismo e con la riduzione della termodinamica classica (con le sue leggi generali piuttosto bizzarre) alla meccanica statistica, nel mondo della scienza si era pensato che, dà lì in poi, si sarebbe trattato solo di applicare l’indagine del mondo fisico a modelli che la riconducessero alle leggi generali già note.

Come sappiamo non è andata così; le nuove scoperte evidenziavano originalità della natura che mal si conciliavano con le leggi note. Per esempio, man mano che si faceva strada (con la scoperta dell’elettrone e con il lavori di Rutherford sulla esistenza di un nucleo atomico) una ipotesi di modello atomico di tipo planetario, nascevano problemi legati al fatto che le cariche elettriche in moto circolare (e dunque accelerato) avrebbero dovuto emettere onde elettromagnetiche perdendo energia e gli atomi planetari sarebbero collassati in una infinitesima frazione di secondo.

Il primo paragrafo riprende quanto già descritto nel capitolo 4 relativamente a questo procedere a tentoni ogni qual volta un nuovo esperimento portava alla scoperta di una nuova bizzarria; pian piano ci si rende conto che bisogna rovesciare il quadro teorico di riferimento e creare qualcosa che la facesse finita con le ipotesi ad hoc.

Il secondo paragrafo è dedicato alle diverse strade che vennero intraprese per arrivare alla nuova teoria: nuove regole costruite a partire solo da grandezze osservabili (Heisenberg), allargamento alla nuova meccanica di quanto era stato fatto in ottica nel passare dall’ottica geometrica all’ottica fisica facendo riferimento ad alcuni schemi teorici (i principi variazionali sviluppati in meccanica razionale) in modo che si potessero applicare al nuovo mondo le leggi e i formalismi matematici delle onde (Schrödinger).

Il secondo approccio si è rivelato più semplice da maneggiare e ancora oggi è quello utilizzato in tutto il mondo per presentare la MQ. Se ne occupa il III paragrafo interamente dedicato alla equazione di Schrödinger: processo euristico che ne giustifica la costruzione, forma matematica e principali caratteristiche (primi cenni agli operatori e significato della funzione di stato Y).

Il quarto e quinto paragrafo hanno una impostazione tecnica e riguardano la manipolazione e l’uso della equazione di Schrödinger: scomposizione in dipendenza spaziale e temporale, costruzione delle soluzioni nel caso di una buca di potenziale finita e infinita. Cercando le soluzioni nel caso della buca finita e nella successiva trattazione della barriera di potenziale avrete l’occasione di capire cosa si intendesse in fisica teorica con lo slogan giù la testa e calcolate.

Per un verso avrete la soddisfazione di capire come salta fuori l’effetto tunnel (uno degli effetti sbalorditivi della MQ) e per l’altro vedrete come la costruzione delle soluzioni sia una cosa concettualmente abbastanza semplice ma operativamente complessa per il continuo ricorso a trucchi, cambi di variabile, costruzione grafica delle soluzioni.

L’ultimo paragrafo tratta esclusivamente dei richiami di matematica necessaria alla trattazione generale della M.Q. di cui si occupa il capitolo successivo.

La MQ, nella sua formulazione generale, ha come protagonisti gli operatori, una generalizzazione del concetto di funzione. Gli operatori (le osservabili) sono oggetti matematici che vengono costruiti in maniera che ad ogni grandezza fisica classica corrisponda un operatore quantistico e sia questo operatore a darci le conoscenze sul mondo fisico; ma, attenzione, esistono anche operatori quantistici che non hanno una grandezza fisica tradizionale corrispondente, per esempio lo spin.

Gli operatori agiscono su oggetti chiamati vettori, che operano nel campo dei numeri complessi e che sono la generalizzazione molto ampia degli ordinari vettori dello spazio a 3 dimensioni.

Tutto ciò avviene in uno spazio astratto, detto spazio di Hilbert e l’ultimo paragrafo del capitolo serve a dare al lettore gli strumenti per comprendere la struttura assiomatica della teoria quantistica di cui si occupa il capitolo 06.

Avrete capito che non è obbligatorio leggere tutto o comunque leggere tutto con lo stesso grado di attenzione relativamente ai dettagli. Tutto dipende dal grado di comprensione che vorrete raggiungere. Questo è il livello di compromesso che mi è sembrato utile e necessario.

Il corso di fisica – le news e gli aggiornamenti del corso – il capitolo 0605