#misurare#

Ieri ho pubblicato su Facebook un post dedicato alla resilienza che mi ha indotto a pensare alla moda delle parole. C'è stato un periodo in cui l'entropia si sprecava e se non dicevi entropia al momento giusto eri poco più che un mentecatto: psicoanalisi, sociologia, economia, politica, relazioni sociali, … oltre naturalmente alla fisica e alla chimica.

Le grandezze fisiche sono una cosa seria e ogni tanto arriva qualcuno che ne sa poco o nulla e le piega al suo genericismo. Per esempio l'entropia, nata dal mondo della termodinamica per spiegare come mai se l'energia in ogni processo si conserva trasformandosi, non si possano invertire le trasformazioni e, volendo, invertire anche la freccia del tempo (dal passato al futuro, ma anche viceversa). L'entropia si connette alla idea di irreversibilità e la cosa più irreversibile con cui abbiamo a che fare è la vita stessa.

La esistenza di una questione energetica, è stata interpretata dalla meccanica statistica nella seconda metà dell'ottocento in termini di evoluzione spontanea verso il livellamento (il disordine è più probabile dell'ordine). Dopo di che la diga si è rotta: bisogna combattere l'entropia dei sentimenti, bisogna diminuire l'entropia di questa classe, il super-io diminuisce l'entropia, ... Per non parlare dell'uso che viene fatto in chiave paragnostica del concetto di energia.

Man mano che invecchio la tendenza a parlare a vanvera mi risulta sempre più insopportabile mentre tra gli strumenti e i luoghi della comunicazione si fa sempre più strada la scorciatoia della volgarizzazione, una specie di aiutino rivolto a quelli che non vogliono pensare.

La società dei consumi ci ha sommerso di sofisticati dispositivi che ci mettono a disposizione, con un click, una quantità enorme di informazioni o di facilities. Come funzionano? Chi lo sa? – Chi li ha pensati? Chi lo sa? Li usiamo perché funzionano. Un pochino ve ne ha parlato Lorenzo Baldi nel suo articolo sulla evoluzione del mondo dei microprocessori (la microelettronica sta per cambiare).

La tecnologia ci permea sempre di più, fa parte del vivere quotidianoma contemporaneamente sembra arretrare la consapevolezza. Avete notato che, a differenza di quanto accadeva una ventina d'anni fa, quando qualunque confezione conteneva, insieme al prodotto, un manuale utente e una guida tecnica di riferimento; manuali spesso più grandi dell'oggetto, si è passati dapprima alla stessa cosa ma messa su CD, poi ai video tutorial su YouTube. Ora sono rimasti solo i quick start dei foglietti in 24 lingue in cui ti spiegano in poche righe come si accende, come si spegne e come fare a contattare il servizio di assistenza. Per fortuna gli smanettoni, grazie alla rete, possono usufruire dei forum, ma anche quelli iniziano a diventare problematici perchè si riempiono di domande cretine e si fatica a separare le informazioni dalla spazzatura.

Se dal mondo degli oggetti passiamo a quello della informazione e della comunicazione il quadro non muta.

Dibattiti televisivi: appena uno degli ospiti cerca di articolare una proposta o dare una spiegazione, interviene solerte l'anchor man di turno, lo blocca, fa capire che chi parla sta annoiando il pubblico e manda la pubblicità non prima di aver riassunto in maniera sbagliata e banale quello che l'ospite cercava di dire.

Invece la scienza, dal punto di vista dei metodi, è passata attraverso una fase classificatoria che rimanda alla teoria degli insiemi (si pensi alla botanica o alla zoologia), per passare ad una fase comparativa basata sulle qualità e sulla relazione di ordinamento (più caldo, meno caldo,  freddino, gradualità dei colori, …), per arrivare infine al metodo quantitativo che, non sempre e in ogni contesto è immediatamente applicabile ma che, trasformando un concetto in una grandezza misurabile rappresenta comunque un punto di arrivo.

Punto di arrivo problematico, visto che non tutto è misurabile sia per ragioni pratiche, sia per ragioni concettuali, e che nei processi di misura e in genere di raccolta dati si aprono tutte le problematiche connesse all'uso della statistica e del calcolo delle probabilità.

Ne ha trattato ampiamente uno dei padri del neopositivismo Rudolf Carnap in I fondamenti filosofici della fisica (Il Saggiatore) e il tema è alla base di una corrente radicale di pensiero (l'operazionismo di Percy Bridgman – 1927) secondo cui la risposta alla domanda relativa a cosa sia una certa grandezza stia nella descrizione del come la si misuri. Brigman era un fisico politicamente impegnato nelle battaglie di Einstein e Russel per il disarmo ed è famoso anche perché è morto suicida nel 1961. Era malato di cancroi allo stadio terminale e si uccise nel suo laboratorio con un colpo di pistola lasciando scritto: «It isn't decent for society to make a man do this thing himself. Probably this is the last day I will be able to do it myself». (credo che sia indecente che la società costringa una persona a farlo da solo. Probabilmente oggi è l'ultimo giorno in cui sarei riuscito a farlo da me).

A proposito di operazionismo ha fatto storia la definizione tranchant di tempo data da Einstein: il tempo è quella cosa che si misura con gli orologi.

Banale? Talmente banale che ne sono venute fuori, il crollo del concetto assoluto di simultaneità per eventi spazialmente distinti, la relatività degli intervalli temporali e delle distanze (più noti come brallentamento degli orologi e contrazione delle lunghezze) mentre l'assoluto si è trasferito ad un livello superiore (il cosiddetto invariante spazio-temporale).

Per le lunghezze la unità di misura è il metro con i suoi multipli e sottomultipli solitamente espressi tramite le potenze del 10, quello che gli scienziati chiamano l'ordine di grandezza. L'esponente della potenza rappresenta il numero di zeri dopo l'1 se è positivo e il numero di posti dopo la virgola se è negativo. Il cambiamento di una unità nell'esponente  vuol dire moltiplicare o dividere per 10. Così 103 = 1'000 mentre 10-3 = 0.001 mentre, passare da 3 a 5 nell'esponente vuol dire spostarsi di due posti e cioè moltiplicare per 100.

Poi ci sono anche le abbreviazioni simboliche, i prefissi, ma non sono indispensabili perché si tratta solo di nomi. (p – pico) sta per 10-12, (n – nano) sta per 10-9, (µ – micro) sta per 10-6, (m – milli) sta per 10-3, (k – chilo) sta per 103, (M – mega) sta per 106, (G – giga) sta per 109, (T – tera) sta per 1012.

Si dirà, ma perché tanta complicazione, in fondo sono così comodi i campi da calcio, le discoteche, le bombe di Hiroshima, i milioni, i bilioni e i trilioni  come criteri di paragone… ? Effettivamente ci sono persone che amano le parole che finiscono in -oni. E allora parliamone. Io sono curioso di capire la ragione per cui parlando di 10 km, in TV si senta dire: pensate, come se metteste in fila tremila automobili. Le automobili, i campi di calcio e le bombe nucleari sono le metafore predilette.

Il nanometro (nm) pari a 10-9 m rappresenta la dimensione degli atomi ed è anche la dimensione cui stanno arrivando le tecnologie della miniaturizzazione in elettronica (le nanotecnologie). Se però vi piace di più 0.000'000'001 lo potete fare. E magari non usate nemmeno quell'apostrofo che serve a dividere in gruppi di 3 per migliorare la lettura, come capita con le banche che ti danno degli IBAN in cui non sai mai quanti sono gli zeri da mettere prima del numero di conto e se cerchi di leggerli ti va insieme la vista.

Con il µm (micrometro) pari a 10-6 m (il millesimo di millimetro) arrivate alle dimensioni dei batteri e anche al limite di funzionamento dei microscopi ottici. Tra i micron e i nano, ci sono i virus, le grandi molecole, il DNA, la vita e la morte … se vi pare poco. In soli tre ordini di grandezza c'è un sacco di roba che interessa i fisici, i biochimici, i virologi, i genetisti. Sono cose di cui conosciamo le leggi fondamentali ma restiamo fregati dalla complessità.

Sapete bene che non c'è solo l'infinitamente piccolo (che viaggia intorno al limite di 10-18 m), c'è anche l'infinitamente grande. In astronomia divulgativa si usa per le distanze interstellari l'anno luce (la distanza che la radiazione elettromagnetica percorre nel vuoto in un anno solare medio) pari a 9.46 × 1015 m (qualcuno direbbe circa 10 milioni di miliardi) o un suo parente stretto che si chiama parsec. A parte il Sole la cui luce impiega circa 8 minuti per arrivare a noi, le stelle più vicine a noi distano qualche anno luce e via a crescere

Ma anche l'anno luce si è rivelato troppo ristretto per chi si occupa di cosmologia, visto che l'universo osservabile è 4,6508 × 1010 anni luce e allora vale la pena di tornare al beneamato metro per dire che l'universo osservabile vale circa 4× 1026 m. Potremmo rifare questi ragionamenti ragionando delle unità di tempo e delle unità di massa e ci renderemmo conto che abbiamo a che fare con una variabilità di diverse decine di ordini di grandezza.

In fisica esistono delle grandezze, dette fondamentali, che noi pretendiamo di considerare invariabili nel tempo e nello spazio e di solito le associamo a qualche fenomeno fondamentale nel cammino della conoscenza umana e alla relativa legge che lo condensa. Quella più famosa è certamente la velocità della luce (e di tutte le onde elettromagnetiche) nel vuoto che indichiamo solitamente con la lettera minuscola c e che vale all'incirca 2.998 × 108 m/s.

Si tratta di una costante davvero importante ed è stato riflettendo sulla sua costanza, non dipendente dallo stato di chi la osserva, che è nata la teoria della relatività. Se stiamo su un auto che si muove con velocità v e lanciamo in avanti un oggetto con velocita V quell'oggetto per un osservatore a terra risulterà avere una velocità v + V. Questo non accade alla luce che si muove con velocità c per tutti gli osservatori.

Mi chiedo e vi chiedo, perché la luce ha proprio quel valore di velocità? L'elettromagnetismo classico consente di prevederne il valore partendo dal alcune costanti sperimentali dei fenomeni elettromagnetici. A prima vista si potrebbe obiettare che quel valore viene a dipendere dalle unità di misura che abbiamo scelto per gli intervalli di tempo e per le lunghezze e il suo valore sarebbe diverso se scegliessimo delle diverse unità. Osservazione ineccepibile, ma a parte la dipendenza dalle unità scelte, un valore esiste. E' quello e solo quello.

Perché con le nostre unità è proprio quello? Come sarebbe il nostro mondo se quel valore fosse diverso? Possiamo solo rispondere che il nostro mondo è fatto così e noi abbiamo la pretesa di dire (questa è la fisica come ricerca di leggi universali) che sarà così anche nei punti dell'Universo in cui non siamo ancora giunti (l'universo è chiuso ma non limitato !).

Ma nella nostra conoscenza del mondo ci sono delle altre sorprese: giocando con le costanti universali abbiamo scoperto che si possono produrre delle altre costanti prive di dimensioni e se una costante è priva di dimensioni vuol dire che il suo valore è sempre lo stesso qualunque sia il sistema di unità che avete usato per misurarla. Quel numero rappresenta una informazione importante sulla natura. Un po' come accade in geometria per il rapporto tra la misura della circonferenza e il suo raggio che vale sempre pigreco (3.1415…) sia che misuriate in metri, in pollici o in quel che vi pare. Ma in questo caso abbiamo a che fare con cose più complesse.

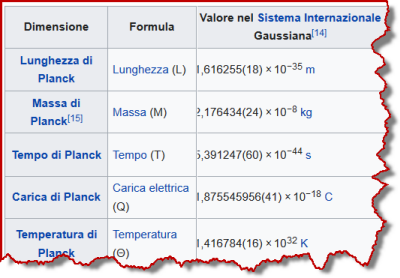
Un'altra cosa che ci intriga è la seguente. Giocando con le costanti universali (la velocità della luce, la carica dell'elettrone che rappresenta il granulo di elettricità, la costante di Planck che connette il tempo alla energia e che fa da mattone del principio di indeterminazione, la costante di Boltzmann che connette la temperatura alla energia, ….) si possono produrre delle costanti dimensionali che hanno le dimensioni di una massa, di un tempo, di una lunghezza.

Noi fisici le chiamiamo grandezze di Planck (le ho riassunte nella immagine di apertura) e ci chiediamo se non debbano essere loro le unità di misura fondamentali anche se, spesso, hanno valori molto diversi dalle unità che abbiamo scelto storicamente dopo secoli di civiltà umana.

Per esempio il metro è stato introdotto quando a fine 700 si è riusciti a misurare un tratto del meridiano di Parigi e si è deciso di fissare una unità che avesse grosso modo le dimensioni di un uomo e corrispondesse ad un numero facile da dire (la quarantamilionesima parte del meridiano, un numero tondo). Tutto ciò naturalmente ha a che fare con la rivoluzione francese e con l'illuminismo.

Poi, nel tempo le m isure si sono fatte più precise e il metro, rimasto identico, ha smesso di di rappresentare un sottomultiplo semplice del meridiano. Sono cambiate tante cose, ora lo si definisce tramite processi di frisica atomica, ma la genesi è rimasta quella. Invece la lunghezza di Planck vale 5,729'475 × 10−35 m, una grandezza piccolissima, e allo stato attuale, nella nostra indagine del mondo noi non sappiamo cosa accada, cosa ci sia, come sia lo spazio a dimensioni inferiori a 10-18 m.

Una bella sfida: dall'infinitamente grande all'infinitamente piccolo grazie alla capacità di pensare e di misurare.

Facebook 5 e 6 agosto 2020

Stamattina tutti a prendere per il culo il Sottosegretario che ha confuso la Libia con il Libano. Ma voi avete ascoltato i servizi radiotelevisivi che assimilavano l'esplosione del deposito di nitrato di ammonio a quella di un ordigno a fissione nucleare?
Sul piano della disinformazione, degli effetti, del tipo di rilascio dell'energia, dell'inquinamento, delle caratteristiche del fungo siamo esattamente allo stesso livello di cretineria.

La parola resilienza l'ho sentita per la prima volta nel corso di tecnologia in terza perito. Era il lontano 1962-1963.
Studiavamo le proprietà dei materiali, in particolare dei metalli, e dunque parlavamo di elasticità, flessibilità, rigidità, fragilità, resistenza alla trazione, resistenza alla compressione, resistenza superficiale, resistenza al taglio e così via.

Si trattava di nomi che volevano condensare una proprietà e molto spesso li si traduceva poi in termini quantitativi attraverso una legge che connettesse sforzo e deformazione.

Poi tutte queste parole, attraverso uno slittamento di ambito di applicazione, sono passate all'economia, alla psicologia, alle Scienze del comportamento o alla sociologia e ogni tanto diventano di moda.

Per esempio la resilienza, oggi molto di moda, sta a indicare, quantificare, o misurare la capacità di adattamento.

Ci sono delle persone che hanno imparato delle parole nuove dall'uso che ne fanno la politica piuttosto che il giornalismo e non si preoccupano di informarsi su origine e significato. Ne ho avuto la prova poco fa, durante la comunicazione al parlamento sullo stato sanitario del paese, da parte del ministro Speranza.

Non si dice capacità di elasticità, capacità di rigidità, capacità di fragilità ma, parlando di sé, di qualcuno, o di un contesto, si dice elasticità rigidità o fragilità. Vale anche per la resilienza. Non c'è la capacità di resilienza, c'è la resilienza e se ti piace capacità dirai capacità di essere resilienti.

Capito, Speranza?