niente paura è solo Schrödinger in compagnia di Hilbert

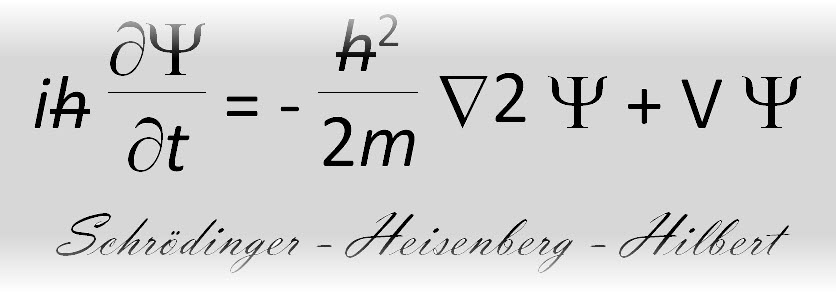
Inizialmente avevo pensato che, per sbrigarmela con la meccanica quantistica in un corso di Fisica Generale, sarebbe bastato un solo capitolo ma non è andata così. I capitoli, abbastanza corposi, sono diventati due e probabilmente per dare conto di tutti gli sviluppi più recenti diventeranno tre.

Questo primo capitolo, nella prima parte riprende la parte introduttiva che avevo scritto quando ancora insegnavo (nel 2007). L’idea è quella di fornire un quadro di quella fase incasinata iniziata a fine XIX secolo e proseguita sino ai primi due decenni del XX.

Dopo che con gli sviluppi della sintesi maxwelliana dell’elettro‌magnetismo e con la riduzione della termodinamica classica (con le sue leggi generali piuttosto bizzarre) alla meccanica statistica, nel mondo della scienza si era pensato che, dà lì in poi, si sarebbe trattato solo di applicare l’indagine del mondo fisico a modelli che la riconducessero alle leggi generali già note.

Come sappiamo non è andata così; le nuove scoperte evidenziavano originalità della natura che mal si conciliavano con le leggi note. Per esempio, man mano che si faceva strada (con la scoperta dell’elettrone e con il lavori di Rutherford sulla esistenza di un nucleo atomico) una ipotesi di modello atomico di tipo planetario, nascevano problemi legati al fatto che le cariche elettriche in moto circolare (e dunque accelerato) avrebbero dovuto emettere onde elettromagnetiche perdendo energia e gli atomi planetari sarebbero collassati in una infinitesima frazione di secondo.

Il primo paragrafo riprende quanto già descritto nel capitolo 4 relativamente a questo procedere a tentoni ogni qual volta un nuovo esperimento portava alla scoperta di una nuova bizzarria; pian piano ci si rende conto che bisogna rovesciare il quadro teorico di riferimento e creare qualcosa che la facesse finita con le ipotesi ad hoc.

Il secondo paragrafo è dedicato alle diverse strade che vennero intraprese per arrivare alla nuova teoria: nuove regole costruite a partire solo da grandezze osservabili (Heisenberg), allargamento alla nuova meccanica di quanto era stato fatto in ottica nel passare dall’ottica geometrica all’ottica fisica facendo riferimento ad alcuni schemi teorici (i principi variazionali sviluppati in meccanica razionale) in modo che si potessero applicare al nuovo mondo le leggi e i formalismi matematici delle onde (Schrödinger).

Il secondo approccio si è rivelato più semplice da maneggiare e ancora oggi è quello utilizzato in tutto il mondo per presentare la MQ. Se ne occupa il III paragrafo interamente dedicato alla equazione di Schrödinger: processo euristico che ne giustifica la costruzione, forma matematica e principali caratteristiche (primi cenni agli operatori e significato della funzione di stato Y).

Il quarto e quinto paragrafo hanno una impostazione tecnica e riguardano la manipolazione e l’uso della equazione di Schrödinger: scomposizione in dipendenza spaziale e temporale, costruzione delle soluzioni nel caso di una buca di potenziale finita e infinita. Cercando le soluzioni nel caso della buca finita e nella successiva trattazione della barriera di potenziale avrete l’occasione di capire cosa si intendesse in fisica teorica con lo slogan giù la testa e calcolate.

Per un verso avrete la soddisfazione di capire come salta fuori l’effetto tunnel (uno degli effetti sbalorditivi della MQ) e per l’altro vedrete come la costruzione delle soluzioni sia una cosa concettualmente abbastanza semplice ma operativamente complessa per il continuo ricorso a trucchi, cambi di variabile, costruzione grafica delle soluzioni.

L’ultimo paragrafo tratta esclusivamente dei richiami di matematica necessaria alla trattazione generale della M.Q. di cui si occupa il capitolo successivo.

La MQ, nella sua formulazione generale, ha come protagonisti gli operatori, una generalizzazione del concetto di funzione. Gli operatori (le osservabili) sono oggetti matematici che vengono costruiti in maniera che ad ogni grandezza fisica classica corrisponda un operatore quantistico e sia questo operatore a darci le conoscenze sul mondo fisico; ma, attenzione, esistono anche operatori quantistici che non hanno una grandezza fisica tradizionale corrispondente, per esempio lo spin.

Gli operatori agiscono su oggetti chiamati vettori, che operano nel campo dei numeri complessi e che sono la generalizzazione molto ampia degli ordinari vettori dello spazio a 3 dimensioni.

Tutto ciò avviene in uno spazio astratto, detto spazio di Hilbert e l’ultimo paragrafo del capitolo serve a dare al lettore gli strumenti per comprendere la struttura assiomatica della teoria quantistica di cui si occupa il capitolo 06.

Avrete capito che non è obbligatorio leggere tutto o comunque leggere tutto con lo stesso grado di attenzione relativamente ai dettagli. Tutto dipende dal grado di comprensione che vorrete raggiungere. Questo è il livello di compromesso che mi è sembrato utile e necessario.

Il corso di fisica – le news e gli aggiornamenti del corso – il capitolo 0605